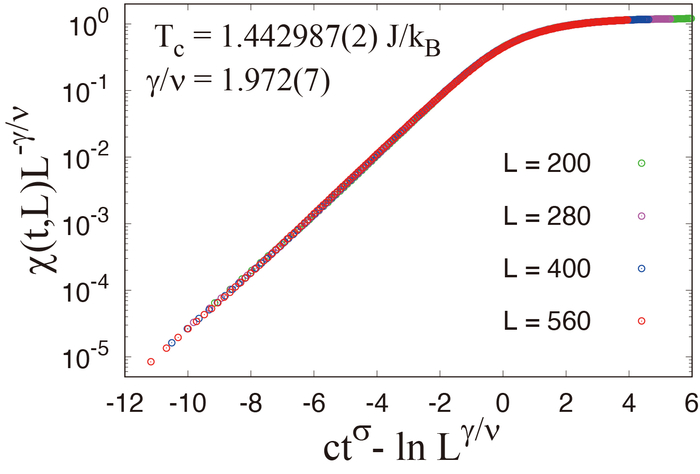
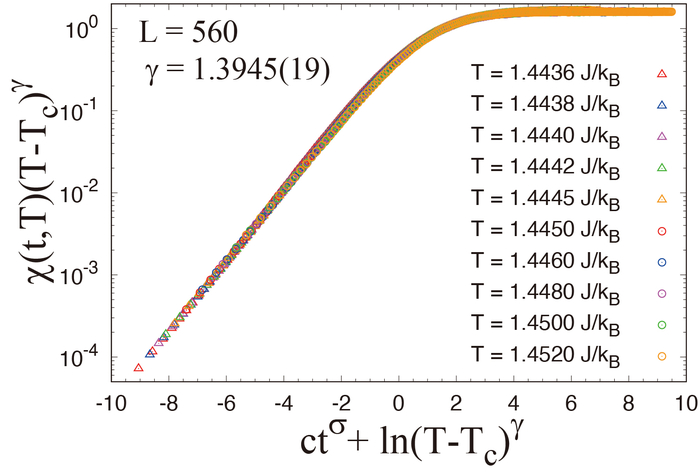
クラスター更新法の転移点における緩和の関数型を調べ、一般的な冪的緩和ではなく引き伸ばされた指数緩和になることを見出して非平衡緩和法と融合した。この関数型は扱いにくいが、初期緩和と平衡状態をつなぐ非平衡-平衡スケーリングを提唱し、平衡状態計算の有限サイズスケーリングと同様の手続きで緩和データを扱えるようにした。左図は等方的スピン系の模型である３次元ハイゼンベルクモデルの帯磁率の転移点におけるスケーリング解析で、転移点と規格化された臨界指数が精度良く得られた。この手法を転移点から離れた緩和データに拡張したのが温度スケーリングである。同モデルの帯磁率をスケーリング解析したのが右図で、左図の転移点を用いて生の臨界指数が精度良く得られた。量子系の平衡状態のモンテカルロ計算は近似的に古典系に射影して行うが、クラスター更新法を用いると厳密な射影が可能になる。従って、非平衡緩和法で量子系を誤差なく扱うには本手法が不可欠である。平衡状態計算では平衡化後の長時間平均で計算精度を上げるが、本手法では乱数列平均で計算精度を上げる。平衡状態計算で不純物効果を扱う際はさらに不純物サンプル平均が必要だが、本手法では不純物平均が乱数列平均の役割を兼ね、二重の平均は不要で計算の手間は不純物を含まない系と同等になる。